Die n-te Wurzel – Beispiele

in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
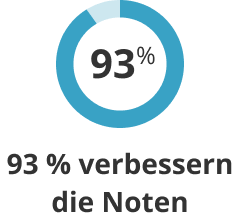
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Die n-te Wurzel – Beispiele
In diesem Video werden Beispiele für unterschiedliche Schreibweisen von n-ten Wurzeln gezeigt. Zuerst werden die Schreibweisen von n-ten Wurzeln und ihrer Kehrwerte wiederholt. Im Anschluss siehst du an Beispielen, wie diese Schreibweisen zur Bestimmung von Lösungen zu n-ten Wurzeln angewendet werden. Die wichtigsten Gesetze zur Umformung von n-ten Wurzeln in Potenzen werden am Ende des Videos noch einmal für dich zusammengefasst.
Die n-te Wurzel – Beispiele Übung
-
Gib die Wurzeln als Potenz mit positivem Exponenten an und bestimme die Lösung.
TippsDie $n$-te Wurzel kehrt das Potenzieren mit $n$ um.
Wenn du wissen möchtest, welchen Wert die $n$-te Wurzel von $a$ hat, musst du überlegen, welche Zahl hoch $n$ $a$ ergibt.
Lösung- Da $2^3=8$ ist, kann man umgekehrt folgern, dass $\sqrt[3]8=8^{\frac13}=2$ ist.
- Da $5^4=625$ ist, kann man umgekehrt folgern, dass $\sqrt[4]{625}=625^{\frac14}=5$ ist.
- Da $3^5=243$ ist, kann man umgekehrt folgern, dass $\sqrt[5]{243}=243^{\frac15}=3$ ist.
-
Berechne die Wurzel.
TippsEs gilt $6^3=216$.
Mit der Rechenregel für Potenzen $(a\cdot b)^n=a^n\cdot b^n$ gilt
$(6\cdot 0,1)^3=6^3\cdot 0,1^3=216\cdot 0,001=0,216$.
Potenzen mit negativen Exponenten können wie folgt umgeschrieben werden:
$a^{-n}=\frac1{a^n}$.
LösungZunächst kann die Schreibweise für den Kehrwert von Wurzeln angewendet werden $\frac1{\sqrt[n] a}=a^{-\frac1n}$:
$\frac1{\sqrt[3]{0,216}}=0,216^{-\frac13}$.
Unter Verwendung einer Regel für das Rechnen mit Potenzen kann weiter umgeformt werden zu
$0,216^{-\frac13}=\frac1{0,216^{\frac13}}$.
Mit der Rechenregel für Potenzen $(a\cdot b)^n=a^n\cdot b^n$ gilt
$(6\cdot 0,1)^3=6^3\cdot 0,1^3=216\cdot 0,001=0,216$. Also ist $0,6^3=0,216$. Damit ist
$\frac1{\sqrt[3]{0,216}}=\frac1{0,6}$.
-
Bestimme zu jeder Potenzschreibweise die Wurzel und berechne die Lösung.
TippsEs gilt:
- $\sqrt[n] a=a^{\frac1n}$ und
- $\frac1{\sqrt[n] a}=a^{-\frac1n}$.
Um die $n$-te Wurzel von $a$ zu berechnen, deren Wert ganzzahlig ist, überlegst du dir, welche Zahl mit $n$ potenziert $a$ ergibt.
Da $2^4=16$ ist, gilt $\sqrt[4]{16}=2$.
Bei der Quadratwurzel wird der Wurzelexponent nicht aufgeschrieben:
$\sqrt[2]{a}=\sqrt{a}$.
LösungWenn die Potenzen bekannt sind, kann umgekehrt die entsprechende Wurzel angegeben werden:
- $4^4=256$, somit ist $4^{\frac14}=\sqrt[4]{256}=4$.
- $16^2=256$, somit ist $256^{\frac12}=\sqrt{256}=16$.
- $3^6=729$, somit ist $729^{\frac16}=\sqrt[6]{729}=3$.
- $9^3=729$, somit ist $729^{\frac13}=\sqrt[3]{729}=9$.
- $8^3=512$, somit ist $512^{\frac13}=\sqrt[3]{512}=8$.
-
Leite den Wert der Potenz $\left(\frac8{27}\right)^{-\frac13}$ her.
TippsEs gilt
$a^{-n}=\frac1{a^n}$.
Wird ein Bruch mit einer negativen Zahl potenziert, so kann man auch den Kehrwert des Bruches mit der positiven Zahl potenzieren:
$\left(\frac ab\right)^{-n}=\left(\frac ba\right)^n$.
Es gilt die Regel für das Rechnen mit Potenzen:
$\left( \frac ab\right)^n=\frac{a^n}{b^n}$.
LösungZur Berechnung von $\left(\frac8{27}\right)^{-\frac13}$ kann zunächst der Kehrwert des Bruches mit dem positiven Exponenten potenziert werden:
$\left(\frac8{27}\right)^{-\frac13}=\left(\frac{27}8\right)^{\frac13}$.
Unter Verwendung von $\left( \frac ab\right)^n=\frac{a^n}{b^n}$ erhält man
$\left(\frac{27}8\right)^{\frac13}=\frac{27^\frac13}{8^\frac13}$.
Da Brüche im Exponenten als Wurzeln geschrieben werden können, lässt sich dieser Term umformen zu
$\frac{27^\frac13}{8^\frac13}=\frac{\sqrt[3]{27}}{\sqrt[3]8}$.
Es gilt
- $3^3=27$ und
- $2^3=8$
$\frac{\sqrt[3]{27}}{\sqrt[3]8}=\frac32=1,5$.
-
Erkläre, wie man die $n$-te Wurzel als Potenz schreiben kann.
TippsEs gilt $\frac1{a^n}=a^{-n}$.
Es gilt $\left(a^{\frac1n}\right)^n=a$.
LösungWurzeln können auch als Potenzen geschrieben werden:
- $\sqrt[n] a=a^{\frac1n}$ und
- $\frac1{\sqrt[n] a}=a^{-\frac1n}$.
Nun können Regeln für das Rechnen mit Potenzen angewendet werden:
$\begin{align*} a^{\frac nn}&=a^{\frac1n \cdot n}\\ &=\left( a^{\frac1n}\right)^n. \end{align*}$
Da die $n$-te Wurzel die Umkehrung des Potenzierens mit $n$ ist, gilt
$\left(\sqrt[n]a\right)^n=a$.
Da die Werte der beiden Potenzen übereinstimmen, müssen auch die Basen übereinstimmen. Es gilt also
$\sqrt[n] a=a^{\frac1n}$.
Da $\frac1{a^n}=a^{-\frac1n}$ ist, kann auch
$\frac1{\sqrt[n] a}=a^{-\frac1n}$
abgeleitet werden.
-
Ermittle den Wert von $4,096^{\frac13}$.
TippsDas Erebnis ist eine Dezimalzahl mit einer Nachkommastelle.
$4096$ ist eine Zweierpotenz: Es gilt $2^{12}=4096$.
Es gilt die Regel für das Rechnen mit Potenzen $(a\cdot b)^n=a^n\cdot b^n$.
$2^4=16$.
LösungDa $2^4=16$ ist und
$4096=2^{12}=\left(2^4\right)^3=16^3$
ist, folgt:
$1,6^3=(16\cdot0,1)^3=16^3\cdot 0,1^3=4096\cdot0,001=4,096$.
Somit ist $4,096^{\frac13}=\sqrt[3]{4,096}=1,6$.
9.385
sofaheld-Level
6.600
vorgefertigte
Vokabeln
7.748
Lernvideos
37.181
Übungen
32.408
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Binomische Formeln
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung
- Quadratische Gleichungen – Übungen
- Flächeninhalt

 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen







